Среди многих интересных сообщений на седьмой конференции по когнитивной науке хочется отметить доклад, который может стать началом для действительно нового и, главное, адекватного с биологической точки зрения подхода к математическому моделированию нервной системы.

На протяжении многих лет основной парадигмой в моделировании мыслительных и поведенческих процессов является коннекционизм – подход, в котором модель представляет собой сложную сеть из связанных между собой относительно простых и одинаковых элементов. Наиболее распространенная форма коннекционизма – искусственные нейронные сети, в которые объединены формальные нейроны. Модель формального нейрона и нейронной сети была предложена У. Маккалоком и У. Питтсом в 1943 году. В то время многие важные свойства нейронов еще не были известны. Нейронные сети успешно применяются в распознавании образов, классификации, кластеризации, прогнозировании, решении ряда вычислительных и оптимизационных задач. Появившиеся в последнее десятилетие «сложные сетевые модели» были успешно применены для описания связей в некоторых биологических и социальных системах, включая сети мозга, где получили название «структурная и функциональная коннектомика» (Bullmore, Sporns 2009; Baronchelli et al 2013).

Однако искусственные нейронные сети и структурная коннектомика все еще имеют мало общего с процессами, происходящими в живых нервных системах. Эти модели основываются на идее «проволочного мозга» (wiring), где он представляется электрической сетью с жестко заданной топологией, которая образуется проводами, соединяющими одинаковые пассивные нейроны. Многие важные свойства, присущие естественным нейронным популяциям, в таких терминах описать невозможно. Современные исследования (Bargmann, 2012; Дьяконова, 2012; Сахаров, 2012) свидетельствуют о том, что (1) наличие разных трансмиттер-специфических нейрональных фенотипов существенно для функционирования естественных нейронных популяций ; (2) как правило, нейроны не только реактивны, но и эндогенно активны, то есть способны генерировать собственную электрическую активность, а не только возбуждаться в ответ на внешний сигнал; (3) выброс трансмиттеров происходит в общее межклеточное пространство, а не только в синаптическую щель; (4) нейротрансмиттерные вещества действуют на нейроны не только фазически ("синаптически"), но и тонически; (5) перестройка топологии сетей и изменение режимов активности нейронов происходят ad hoc – под действием разных нейротрансмиттеров.

В лаборатории О.П. Кузнецова (ИПУ РАН) ищут подходы к математическому моделированию этих, принципиальных для функционирования реальной нервной системы, свойств. Л.Ю. Жилякова предложила модель, в которой формальный нейрон обладает не только электрическим зарядом, но и химическими входами (рецепторами к разным нейротрансмиттерам) и химическим выходом (секретируемый нейротрансмиттер или набор нейротрансмиттеров). Нейроны в этой модели «разноцветны», отличаются по входам и выходам, т.е. секретируют разные нейротрансмиттеры и по-разному реагируют на разные химические сигналы. Кроме того, они «не пассивны», обладают собственной, а не только вызванной активностью. Сеть из таких нейронов названа гетерогенной нейронной сетью. При этом термин «сеть» не означает наличия лишь электрических связей – любая химическая связь в ней может быть отражена теми же математическими средствами. Каждый значимый в этой сети трансмиттер может выделить свою подсеть. Переключение между сетями производится с учетом пороговых характеристик. Модель, обладающая такими свойствами, порождает сети с топологией, способной динамически изменяться при изменении концентраций тех или иных трансмиттеров в среде.

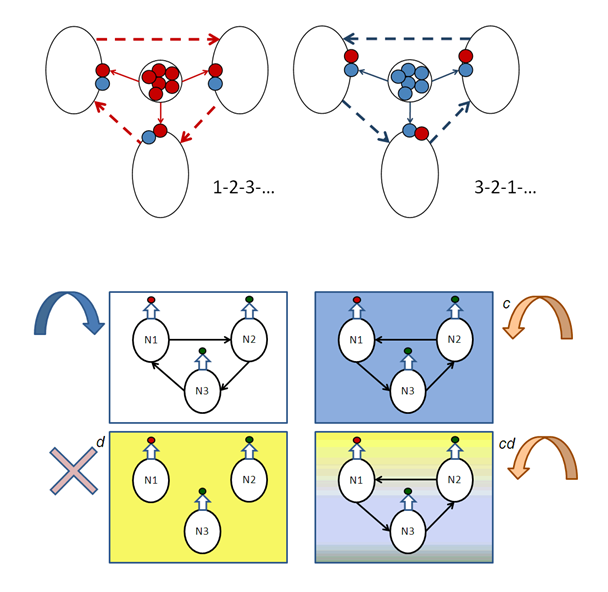
Уже сформулирована модель для простого моторного генератора (3 нейрона, 3 фазы ритма, 2 внутренних и 2 внешних нейротрансмиттера, способность к перестроению). Эта модель соответствует реальным биологическим характеристикам известных центральных генераторов паттерна (Central Pattern Generators). Так, появление в модели «эндогенной активности» у нейронов автоматически привело и к доминированию тормозных (как в биологических генераторах), а не возбуждающих (как в прежних сетевых моделях) связей. Наличие межклеточной среды и разноцветного нейромодуляторного фона к трансмиттер-специфическим перестройкам, сходными с наблюдаемыми в реальности. И, наконец, жесткие анатомические связи оказались не необходимыми для ее работы, такой генератор «связан» химически изначально, что соответствует реальному онтогенезу нервной системы, при котором нейротрансмиттерная специфичность задается до установления синаптических связей. Помимо перечисленных преимуществ, модель дала ответ на частный, но давний нейробиологический вопрос: как при объемной несинаптической секреции нейротрансмиттеров генератор трех фаз поведения может работать не на трех, а на двух разных нейротрансмиттерах?

Основная работа – еще впереди. На сегодняшний день важно то, что шаг в этом необходимом и правильном направлении, наконец, сделан. Нейробиологи и медики могут надеяться на биологически адекватное математическое моделирование реальных нейронных взаимодействий. А поскольку уже есть первые попытки создания физических аналогов хемочувствующих и хемосекретирующих нейронов для протезирования нервной системы, появляется вероятность использования гетерогенной нейронной сети не только в фундаментальной, но и в прикладной науке.

Bargmann, C.I. Beyond the connectome: how neuromodulators shape neural circuits. Bioessays 34, 458–465 (2012).

Baronchelli, A., Ferrer-i-Cancho, R., Pastor-Satorras, R., Chater, N., Christiansen, M.H. Networks in Cognitive Science // Trends in Cognitive Sciences. July 2013, Vol. 17, No. 7

Bullmore, E. Sporns, O. Complex brain networks: graph theoretical analysis of structural and functional systems // Nature Reviews Neuroscience 10, 186-198 (March 2009).

McCulloch W.S., Pitts W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys., 1943, v.5, pp.115-133. (Рус. пер. Маккаллок У.С., Питтс У. Логическое исчисление идей, относящихся к нервной активности. // В кн. Автоматы. Под ред. К.Э.Шеннона и Дж.Маккарти. М., ИЛ, 1956, с. 362-384).

Дьяконова В.Е. Нейротрансмиттерные механизмы контекст-зависимого поведения // Журнал высшей нервной деятельности, 2012, том 62, № 6. С. 1–17.

Жилякова Л.Ю. Сетевая модель распространения нескольких видов активности в среде сложных агентов и её приложения // Онтология проектирования. 2015. Том 5. №3(17). С. 278-296.

Сахаров Д.А. Биологический субстрат генерации поведенческих актов // Журнал общей биологии. Том 73, № 5, Сентябрь-октябрь, 2012. С. 334–348.

Новость подготовила © 2016 Дьяконова В.Е.
07.07.2016