Процесс индивидуального развития сопровождается выраженным изменением формы эмбриона, в основе которого лежат как локальные, так и достаточно масштабные деформации тканей. Согласно законам классической механики источником деформации может является только механическая сила [1,2], поэтому детальное изучение механизмов эмбрионального формообразования должно включать в себя, в том числе, исследование локализации и возникновения сил, приводящих к этим деформациям [3]. Если в случае локальных деформаций можно ограничиться исследованием клеточной активности, лежащей в их основе, то в случае крупномасштабных деформаций необходимо установить, как именно механическая сила распространяется через толщу ткани. Без знания механических свойств конкретного типа биологической ткани невозможно в полной мере ответить на этот вопрос [4].

Концептуально, исследование механических свойств ткани технически сводится к регистрации её ответа на приложение механической силы. Поэтому, особый интерес в контексте методологии механобиологических исследований представляет совершенствование методов контролируемого приложения механической силы к биологической ткани. Одним из наиболее новых является метод, предложенный Serwane с соавт. [5]. В отличие от разработанных ранее, он обладает наименьшим количеством ограничений, в частности, он применим для исследования интактных эмбрионов, не приводит к выраженной деформации образца, а также не имеет ограничений в виде минимально необходимого объёма ткани или необходимости работать только с поверхностью ткани. Суть метода заключается в инъекции в эмбрион (Serwane с соавт. провели своё исследование на эмбрионе рыбки Данио (Danio rerio)) на ранних стадиях развития биосовместимых ферромагнитных микрокапель, которые можно деформировать магнитным полем. Действие на микрокаплю магнитного поля заданной напряжённости H приводит к её удлинению: изначально шарообразная капля меняет форму на эллипсоидальную (Рис. 1, a). Деформации микрокапли противодействуют вязкоупругие свойства окружающего её материала эмбриона (Рис. 1 b).

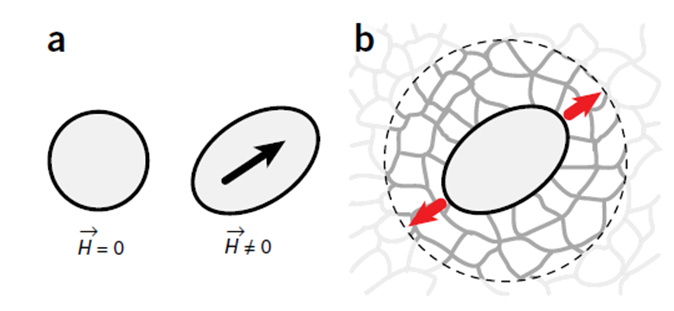
Рис. 1. Применение ферромагнитных микрокапель для исследования механических свойств биологических тканей: воздействие магнитным полем приводит к изменению формы капли (a), в результате чего капля деформирует окружающую её ткань (b) с силой, определяемой напряженностью H магнитного поля.

Зная численное значение силы, с которой деформированная микрокапля действует на прилежащую ткань (её можно рассчитать, зная напряженность магнитного поля H и механические свойства самой капли), и измерив результирующую деформацию в материале эмбриона, окружающем каплю, можно вычислить параметры, отражающие механические свойства исследуемой ткани.

В самом простом варианте сила F и возникающая под её действием деформация ε связаны друг с другом через соотношение вида

F ~ kε	(1)

Чтобы измерить механические параметры ткани k, необходимо экспериментально установить, какую деформацию ε в данном типе эмбриональной ткани способна вызвать сила фиксированной величины F. После этого механические параметры ткани можно вычислить из соотношения (1). В целом этот принцип и лежит в основе метода, предложенного Serwane с соавт.

Соотношение (1) является упрощением и представлено для иллюстрации работы метода. Реальный вид соотношения будет зависеть от конкретной модели, которую исследователь выберет для описания исследуемого материала. Однако, даже при построении более сложных моделей (как и в случае данной работы), отталкиваются от двух идеализированных случаев: идеально упругого тела и идеальной Ньютоновской жидкости [2].

При действии силы на идеально упругое тело, в нём возникают механические напряжения, которые стремятся вернуть тело к изначальной форме (механическое напряжение σ – это частное силы F, действующей перпендикулярно поперечному сечению S тела, и площади поперечного сечения, σ = F/S). Поэтому после прекращения действия силы тело восстанавливает исходную форму. В этом случае, возникающее в ткани напряжение (а, значит, и величину действующей на ткань силы) можно однозначно определить через деформацию:

σ = Eε	(2)

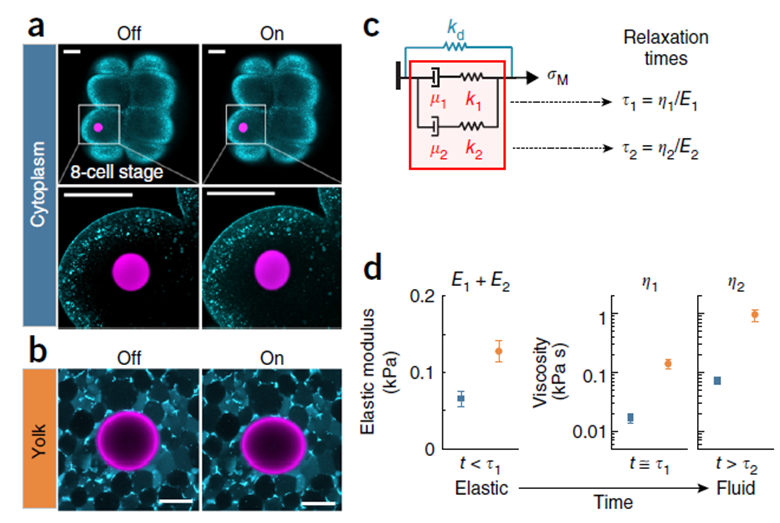
Рис. 2. Исследование механических свойств на субклеточном масштабе в раннем развитии Danio rerio. a,b - конфокальные изображения, демонстрирующие ферромагнитную микрокаплю (сиреневый) внутри бластомера на восьмимиклеточной стадии (a) и желточной клетке в промежутке между одно- и восьмиклеточной стадией, Off – до деформации магнитный полем, On – в пиковой точке деформации, c – реологическая модель, описывающая механические свойства цитоплазмы бластомеров и желточной клетки, d – экспериментально установленные механические параметры (модуль упругости E и вязкость η) цитоплазмы бластомера (синий) и желточной клетки (оранжевый), вязкость η измерена для двух временных точек.

Жидкостью, в физическом смысле, считается вещество, способное неограниченно деформироваться под действием приложенной силы [6]. Действие силы приводит к возникновению в жидкости касательных напряжений, под действием которых частицы жидкости меняют взаимное расположение. Такие перестройки, в свою очередь, приводят к релаксации напряжений, а частицы жидкости сохраняют изменённое расположение после прекращения действия силы. Так как жидкости способны неограниченно деформироваться под действием силы, механические напряжения будут определяться не деформацией ε, а тем, насколько быстро под действием силы частицы меняют своё расположение dε со временем dt, т.е. скоростью деформации

.

То, насколько взаимодействие между частицами в конкретном веществе замедляет скорость деформации при заданной величине силы, задаётся через вязкость η. Таким образом, напряжение будет иметь вид:

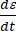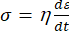	(3)

Общий вид наименее сложной модели (двухкомпонентная модель Максвелла), которая оказалась способна описать временную динамику механических свойств выбранных структур эмбриона, является комбинацией соотношений (2) и (3) (Рис. 2 c). На Рис. 2 элементы модели, описываемые соотношением (2), представлены в виде пружин (k₁ и k₂), а соотношением (3) – демпферов (µ₁ и µ₂).

Именно модуль упругости Е из соотношения (2) и вязкость η из соотношения (3) и являются ключевыми механическими параметрами, которые были установлены в работе Serwane (Рис. 2 d, Рис. 3 c). При этом авторы продемонстрировали, что величина модуля упругости, ровно, как и значение вязкости, оказались ниже в зоне мезодермы хвостовой почки развивающегося эмбриона (Рис. 3a, PZ, Рис. 3c, розовые маркеры) по сравнению с более антериорной областью пресомитной мезодермы (Рис. 3a, PSM, Рис. 3c, розовые маркеры). Чтобы понять клеточные механизмы, опосредующие подобную разницу в механических свойствах тканей, авторы предприняли дополнительные эксперименты [7]. Для этого они оценили подвижность клеток в мезодерме хвостовой почки и пресомитной мезодерме. Клетки мезодермы хвостовой почки в 6 раз чаще меняли соседей, а флуктуация длины клеточных контактов между соседними клетками была гораздо более выражена. Такая повышенная частота клеточных перегруппировок в клетках мезодермы хвостовой сопровождалась сниженным уровнем межклеточной адгезии и большим размером межклеточного пространства по сравнению с пресомитной мезодермой. Авторам удалось достаточно элегантно продемонстрировать это с помощью линии, нокаутной по гену N-кадгерина. У этой нокаутной линии размеры межклеточных пространств оставались неизменными в мезодерме хвостовой почки, но увеличивались в пресомитной мезодерме по сравнению с диким типом. Это позволило авторам сделать вывод о меньшей интенсивности межклеточной адгезии в области мезодермы хвостовой почки, т.к. нокаут по N-кадгерину её практически не нарушал. Таким образом, большую жесткость ткани в области пресомитной мезодермы можно объяснить более выраженной N-кадгерин-зависимой адгезией и, как следствие, меньшей подвижностью клеток внутри ткани. При этом, в области мезодермы хвостовой почки менее выраженная межклеточная адгезия создает возможность для более интенсивных перегруппировок клеток, из-за чего ткань релаксирует возникающие в ней напряжения, подобно частицам в жидкости. Этот результат хорошо согласуется с уже озвученными данными о меньшей величине коэффициента вязкости η в области мезодермы хвостовой почки, т.к. в жидкости с меньшей вязкостью частицы более подвижны (Рис 3c, розовые маркеры).

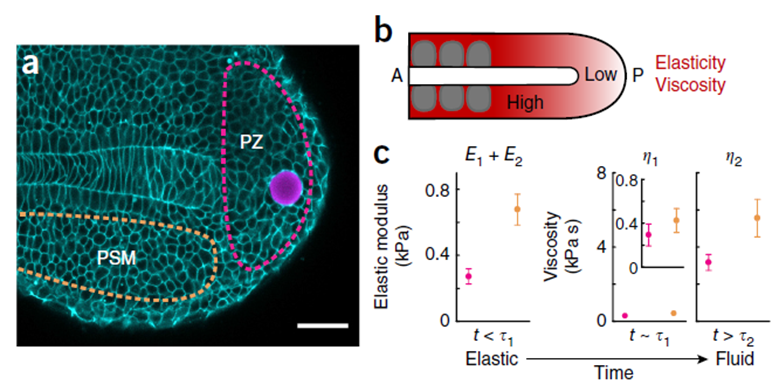
Рис. 3. Исследование механических свойств на тканевом масштабе в раннем развитии Danio rerio. a - конфокальное изображения, демонстрирующие ферромагнитную микрокаплю (сиреневый), попавшую в состав мезодермы хвостовой почки (PZ, розовая пунктирная линия), PSM – пресомитная мезодерма (оранжевая пунктирная линия), b – схематическое изображение пространственных различий в механических свойствах тканей на стадии хвостовой почки: наиболее постерионые ткани характеризуются меньшей вязкостью и упругостью по сравнению с более антериорными, расположенными вблизи формирующихся сомитов, с – экспериментально установленные механические параметры (модуль упругости E и вязкость η ) мезодермы хвостовой почки (розовый) и пресомитной мезодермы (оранжевый) ), вязкость η измерена для двух временных точек.

Сами авторы отмечают, что данный метод позволит в будущем установить, как специфические молекулярные каскады влияют на механический статус ткани. Помимо чисто фундаментальных исследований, метод Serwane с соавт. также, может быть, использован в тканевой инженерии при создании матриксов с механическими свойствами, максимально приближёнными к таковым in vivo. Однако, данный метод может оказаться применим для решения ещё одного спектра задач: в перспективе, он позволит более точно оценить механические силы, регистрируя только возникающие в ткани деформации: измерив значения E и η для конкретного типа ткани и конкретной стадии развития, появляется возможность через соотношения (2) и (3) оценивать напряжения σ, регистрируя только возникающие в ткани деформации (или их скорость). Сама по себе регистрация (скорости) деформаций позволяет только качественно охарактеризовать соотношение сил в различных участках эмбриона, но, в противоположность измерению механических сил, охарактеризовать деформации гораздо проще в силу неинвазивности большей части методов. В частности, для этого достаточно просто визуализировать отдельные структуры внутри ткани (например, мембраны клеток), а сам процесс регистрации может сводиться к анализу цифровых изображений [например, 8]. Получение же численных данных о механических свойствах ткани позволит более доказательно оценить роль механических сил в развитии. Например, это позволило бы ответить на вопрос о том, насколько устойчивым инструментом регуляции развития являются механозависимые сигнальные каскады благодаря возможности оценить, как механические свойства тканей варьируют от эмбриона к эмбриону внутри хотя бы одного вида [9].

1. Murray J.D. Mathematical Biology biomedical applications // Mathematical Biology II - Spatial Models and Biomedical Applications. 2003. 814 p.
2. Davidson L.A. Embryo Mechanics. Balancing Force Production with Elastic Resistance During Morphogenesis // Current Topics in Developmental Biology. 1st ed. Elsevier Inc., 2011. Vol. 95. 215–241 p.
3. Dance A. The secret forces that squeeze and pull life into shape // Nature. 2021. Vol. 589, № 7841. P. 186–188.
4. Stooke-Vaughan G.A., Davidson L.A., Woolner S. Xenopus as a model for studies in mechanical stress and cell division // Genesis. 2017. Vol. 55, № 1–2. P. 1–11.
5. Serwane F. et al. In vivo quantification of spatially varying mechanical properties in developing tissues // Nat. Methods. 2017. Vol. 14, № 2. P. 181–186.
6. Janmey P.A., Georges P.C., Hvidt S. Basic Rheology for Biologists // Methods in Cell Biology. 2007. Vol. 83.
7. Mongera A. et al. A fluid-to-solid jamming transition underlies vertebrate body axis elongation // Nature. Springer US, 2018. Vol. 561, № 7723. P. 401–405.
8. Heller D. et al. EpiTools: An Open-Source Image Analysis Toolkit for Quantifying Epithelial Growth Dynamics // Dev. Cell. Elsevier Ltd, 2016. Vol. 36, № 1. P. 103–116.
9. Von Dassow M., Davidson L.A. Physics and the canalization of morphogenesis: A grand challenge in organismal biology // Phys. Biol. 2011. Vol. 8, № 4. P. 1–29.

Новость подготовил © Бредов Д.В.
04.03.2021